Matrices especiales

Las matrices son esenciales en las matemáticas, debido a que se utilizan en distintas áreas. por ende, las matrices tienen determinadas características propiedades y tipos, a continuación se mostrarán algunos tipos de matrices.

• Matriz de identidad: 

La matriz identidad de dimensión $n$, $I_n$, es la matriz de dimensión $nxn$ formada por 1's en la diagonal principal y 0's en las restantes posiciones. En otras palabras, la matriz solo tiene 1's en su diagonal y el resto de los elementos son 0's, también se reconoce por ser una matriz cuadrada.

ejemplo:

• Matriz diagonal:

La matriz A=Aij se denomina diagonal cuando todos los elementos que no están en la diagonal son 0.

Ejemplo:

1) Matriz Bidiagonal:Una matriz bidiagonal es una matriz cuadrada en la que todos los elementos que no son de la diagonal principal o de la diagonal superior o inferior son 0. como por ejemplo: 

Matriz Bidiagonal superior

Matriz Bidiagonal inferior

2)Matriz Tridiagonal:Una matriz tridiagonal es una matriz cuadrada cuyos únicos elementos diferentes de cero son los de la diagonal principal y de las diagonales adyacentes por arriba y por debajo. Como por ejemplo:

• Matriz triangular: 

Dentro de este tipo de matrices está la matriz triangular superior y la matriz triangular inferior, Una matriz triangular superior es cuando tiene 0's por debajo de la diagonal y, cuando se encuentran los 0's por encima de la diagonal es una matriz triangular inferior, Ejemplos:

Matriz triangular superior.

Matriz triangular inferior.

• Matriz transpuesta: 

La matriz traspuesta de una matriz $A$$A$ de dimensión $m$$x$$n$$mxn$ es una matriz de dimensión $n$$x$$m$$nxm$ que tiene por columnas a las filas de $A$$A$. Se denota como $A^{}$${}^{}$$A^T$ (o $A^{}$${}^{}$$A^{\prime }$ si la matriz es real).
Por ejemplo,

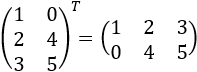
• Matriz simétrica: 

La condición para que una matriz sea simétrica es que su transpuesta sea igual. Por ejemplo: